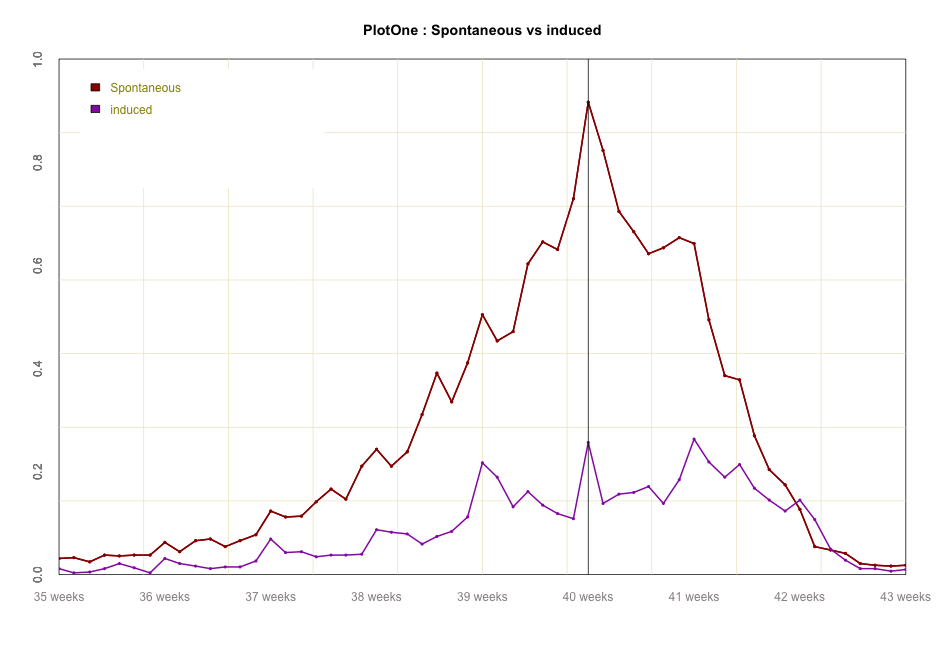
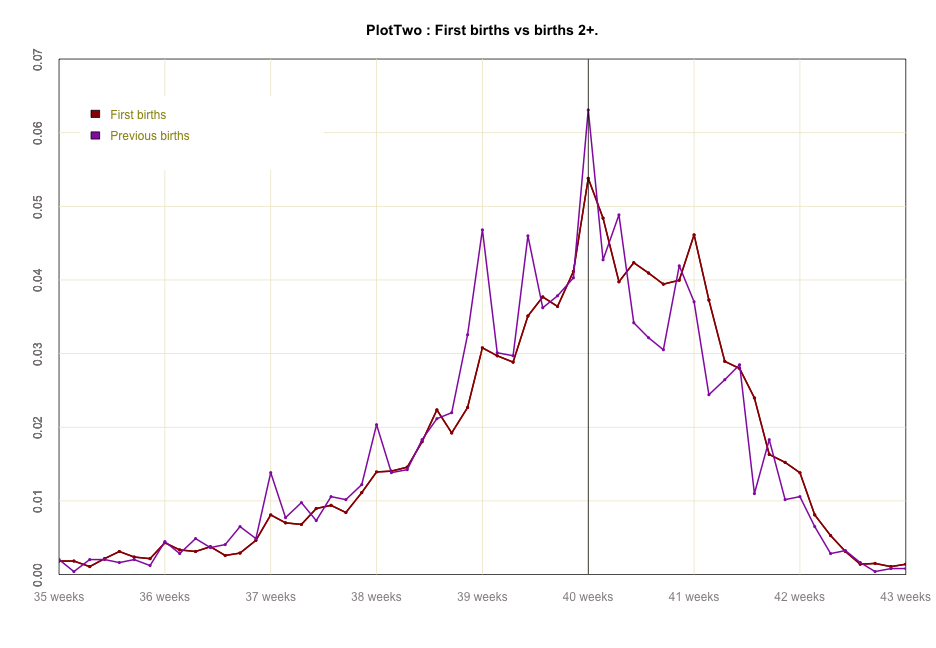
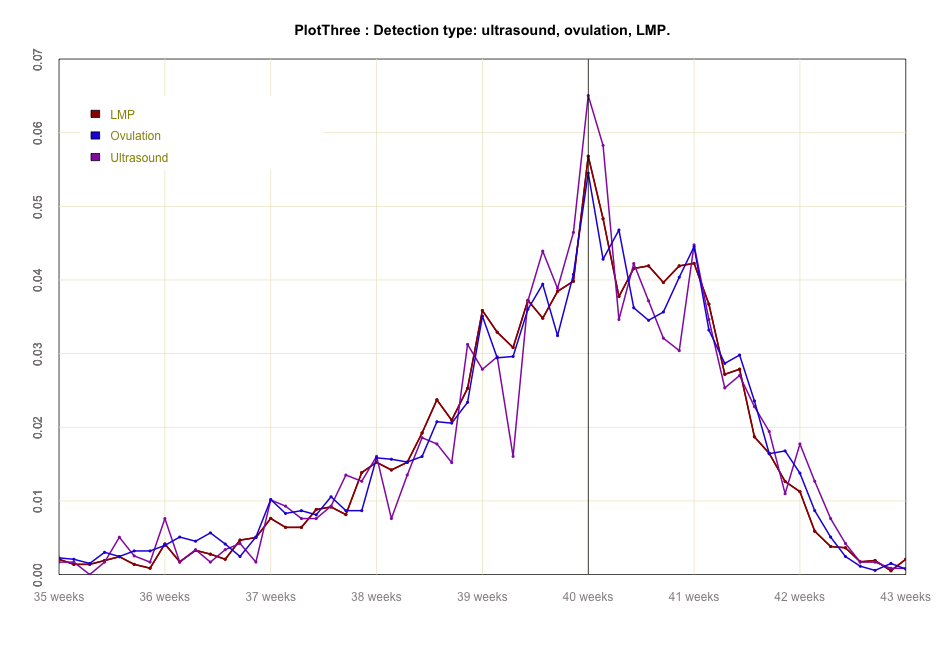
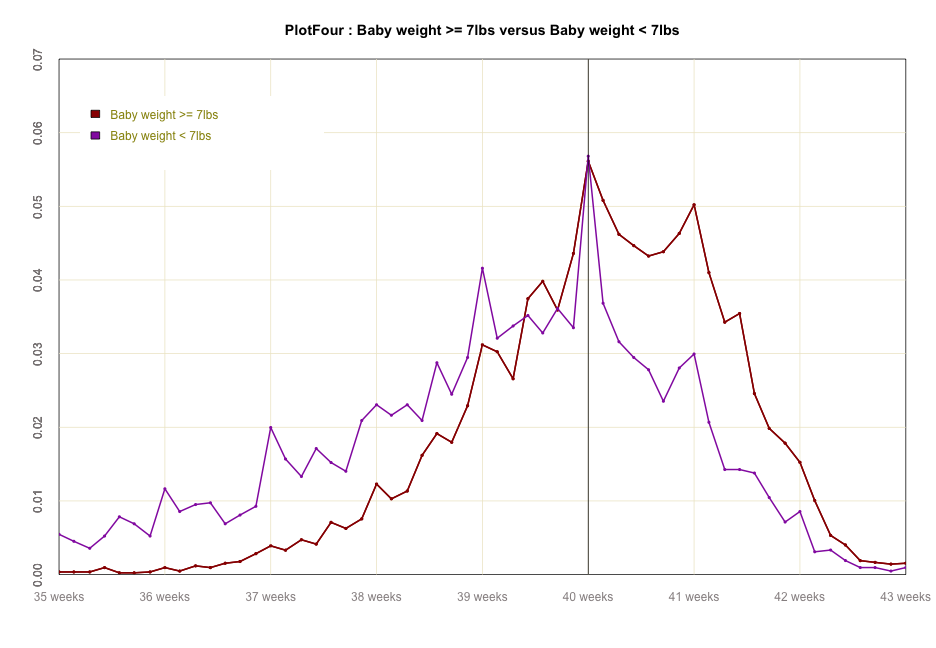
#global code
##global adjustments starts 01
rm(list=ls())
#seed for replication
set.seed(100)
oldwarnval <- getOption("warn") #preserve old value
options(warn = -1) #warnings are silent now

##global adjustments ends 01


#####generalized plot function
plotFunction <- function(x1,y1,x2,y2,x3 = -1,y3
                         ,ztitle = "plot"
                         ,zlegendText = c("var1","var2")
                         ,customYlim = c(0,7/100)
                         ,customLegend = c(35.2,37.5,0.065, 0.055)
                         ,customGrid = c(8,7)
                        ){
  #X fisrt line plot
  #Y second line plot  
  #Z thir line plot
  x = x1;y = y1;
  plot(x,y
       ,type= "o"
       ,main= ztitle
       ,col = rgb(6/10, 0, 0)  #36,137,371 #color of the line chart
       ,lwd = 2                  #line thickness
       ,pch = 19                  # add points, solid circle,
       ,cex = 0.3                # size of the point on the chart
       ,tick = F
       ,xaxs = "i"
       ,yaxs = "i"
       ,xaxt = "n"
       ,ylim = customYlim
       ,xlab = ""
       ,ylab = ""
  )  #customGrid = c(8,7)
  grid(nx = customGrid[1]#8
       ,ny = customGrid[2]#7
       , lty=1, col = "cornsilk2")

  lines(x, y
        ,type= "o"
        ,col = rgb(6/10, 0, 0)  #36,137,371 #color of the line chart
        ,lwd = 2                  #line thickness
        ,pch = 19                  # add points, solid circle,
        ,cex = 0.3                 # size of the point on the chart
  )
  x = x2; y = y2;
  lines(x, y
        ,type= "o"
        ,col = rgb(149/255, 41/255, 176/255)
        ,lwd = 2
        ,pch = 19
        ,cex = 0.3
  )
  if(x3 != -1){
    x = x3; y = y3;
    zcol <- c((rgb(6/10, 0, 0)), rgb(36/255, 29/255, 219/255),
      rgb(149/255, 41/255, 176/255)) #3 colors
    zcol1 <- rgb(36/255, 29/255, 219/255)
    lines(x, y, type = "o"
          ,col.lab="blue"
          ,col = zcol1
          ,lwd = 2
          ,pch = 19
          ,cex = 0.3
    )
  }else{
    x = 0; y = 0;
    zcol <- c((rgb(6/10, 0, 0)), rgb(149/255, 41/255, 176/255)) # 2 colors
  }

  axis(side = 1, at = 35:43
       ,labels = paste(c(35:43),"weeks")
       ,col.axis = rgb(151/255, 145/255, 145/255)
       ,tick = F
  )
  axis(side = 2
       ,col.axis = rgb(151/255, 145/255, 145/255)
       ,tick = F
  )
  legend( x = c(customLegend[1],customLegend[2] )
         ,y = c(customLegend[3],customLegend[4] ) #x=c(35.2,37.5),y=c(0.98, 0.75)
         ,legend = zlegendText
         ,fill = zcol
         ,text.col = rgb(151/255, 145/255, 10/255)
         ,border = 1
         ,box.lty= 0
         ,bty = "o"
         ,y.intersp=1.5
  )
  abline(v = 40)

  #return(1)
}
#read file
df <- data.frame(read.csv("~/Downloads/Tony/Project 1/sf_gestationdata.csv",stringsAsFactors = F))

#elmininate date based on exclude column
df <- df[df$exclude == 0,]
#slimmer dataFrame
df02 <- df[,c("id", "motherbirthyear", "multiples", "pounds", "bornonday"
              , "duedatebase", "induced", "exclude", "previousbirths")]

#head at a glance
head(df02)

summary(df02)

####Working with the data.
#add week column to the df
df02$week <- round(df02$bornonday/7,02) #revisit # week generation
####plotOne
#add Spontaneous column to the table
df02$Spontaneous <- ifelse(df02$induced == 1,0,1)
#aggregate table to plot
df03induced <- aggregate(induced ~ week,FUN = sum, data = df02[,c("week","induced","Spontaneous")])
df03spontaneous <- aggregate(Spontaneous ~ week,FUN = sum, data = df02[,c("week","induced","Spontaneous")])

#data frames to plot One 
df03induced <- df03induced[df03induced$week >= 35.00 & df03induced$week <= 43.00,]
df03spontaneous <- df03spontaneous[df03spontaneous$week >= 35.00
                                    & df03spontaneous$week <= 43.00,]
#normalizing the axis 
normFactor <- max(df03spontaneous$Spontaneous) + 51 #normalize
df03spontaneous$Spontaneous <- df03spontaneous$Spontaneous/normFactor
#normFactor <- max(df03induced$induced) #normalize
df03induced$induced <- df03induced$induced/normFactor

#custom parameters
customYlim = c(0,1)
customLegend = c(35.2,37.5,0.98, 0.75)
customGrid = c(10,7)
#plot One 
plotFunction(x1 = df03spontaneous$week, y1 = df03spontaneous$Spontaneous,
             x2 = df03induced$week , y2= df03induced$induced,
             ztitle = "PlotOne : Spontaneous vs induced",
             zlegendText = c("Spontaneous","induced"),
             customYlim = customYlim,
             customLegend = customLegend,
             customGrid = customGrid
)

#### plotTwo
# First births vs births 2+
# head(df02)
#new dfs for plots # weeks in [35,43]
df04fb <- df02[df02$previousbirths == 0 & df02$week >=35.00 & df02$week <=43.00,]  #"first Birth df"
df04pb <- df02[df02$previousbirths == 1 & df02$week >=35.00 & df02$week <=43.00,]  #"Previous Birth df"

#aggregate tables
df04fbA <- aggregate(previousbirths ~ week,FUN= length , df04fb[,c("week","previousbirths")] )
df04pbA <- aggregate(previousbirths ~ week,FUN= length , df04pb[,c("week","previousbirths")] )

#count to be normalized
count <- sum(df04fbA$previousbirths)
df04fbA$previousbirths <- df04fbA$previousbirths/count #normalization with count
count <- sum(df04pbA$previousbirths)
df04pbA$previousbirths <- df04pbA$previousbirths/count #normalization with count

#plotTwo
plotFunction(x1 = df04fbA$week, y1 = df04fbA$previousbirths,
             x2 = df04pbA$week, y2= df04pbA$previousbirths,
             ztitle = "PlotTwo : First births vs births 2+.",
             zlegendText = c("First births","Previous births")
)

####Plot 3
#Detection type:Ultrasound vs Ovulation vs LMP
#head(df02)
unique(df02$duedatebase)

df05 <- df02[df02$duedatebase=="LMP"             #df for ploting
               | df02$duedatebase=="ultrasound"
               | df02$duedatebase=="ovulation",]

#dummy columns
df05$LMP <- ifelse(df05$duedatebase == "LMP",1,0) #LMP column
df05$ultrasound <- ifelse(df05$duedatebase == "ultrasound",1,0) #ultrasound column
df05$ovulation <- ifelse(df05$duedatebase == "ovulation",1,0) # Ovulation

#aggregate tables
df05Lmp <- aggregate(LMP ~ week,FUN= sum , data = df05[,c("week","LMP","ultrasound","ovulation")])
df05ultrasound <- aggregate(ultrasound ~ week,FUN= sum , data = df05[,c("week","LMP","ultrasound","ovulation")])
df05ovulation <- aggregate(ovulation ~ week,FUN= sum , data = df05[,c("week","LMP","ultrasound","ovulation")])

#remove weeks !in [35.00,43.00]
df05Lmp <- df05Lmp[df05Lmp$week >= 35.00 & df05Lmp$week <= 43.00,]
df05ultrasound <- df05ultrasound[df05ultrasound$week >= 35.00 & df05ultrasound$week <= 43.00,]
df05ovulation <- df05ovulation[df05ovulation$week >= 35.00 & df05ovulation$week <= 43.00,]

#counter to normalize the table
count = sum(df05Lmp$LMP)
df05Lmp$LMP <- df05Lmp$LMP/count #nomalize 
count = sum(df05ultrasound$ultrasound)
df05ultrasound$ultrasound <- df05ultrasound$ultrasound/count
count = sum(df05ovulation$ovulation)
df05ovulation$ovulation <- df05ovulation$ovulation/count

#plotThree
plotFunction(x1 = df05Lmp$week, y1 = df05Lmp$LMP,
             x2 = df05ovulation$week , y2= df05ovulation$ovulation,
             x3 = df05ultrasound$week, y3= df05ultrasound$ultrasound,
             ztitle = "PlotThree : Detection type: ultrasound, ovulation, LMP.",
             zlegendText = c("LMP","Ovulation", "Ultrasound")
)

#####plotFour
#Baby weight >= 7lbs versus Baby weight < 7lbs
#head(df02,20)
df02$poundsGT7 <- ifelse(df02$pounds >=7, 1, 0) #dummy column
df06b7 <- df02[df02$poundsGT7 == 0,c("week","poundsGT7")]  #below 7
df06a7 <- df02[df02$poundsGT7 == 1,c("week","poundsGT7")]  #above 7

#week within 35 to 43
df06b7 <- df06b7[df06b7$week >= 35.00 & df06b7$week <=43.00,]
df06a7 <- df06a7[df06a7$week >= 35.00 & df06a7$week <=43.00,]

#aggregate tables for ploting
df06b7tab <- aggregate(poundsGT7 ~ week ,FUN = length, data = df06b7) # below 7
df06a7tab <- aggregate(poundsGT7 ~ week ,FUN = length, data = df06a7) # above 7

#count for normalize
count <- sum(df06b7tab$poundsGT7)
df06b7tab$poundsGT7 <- df06b7tab$poundsGT7/count
count <- sum(df06a7tab$poundsGT7)
df06a7tab$poundsGT7 <- df06a7tab$poundsGT7/count

#PlotFour : Baby weight >= 7lbs versus Baby weight < 7lbs
plotFunction(x1 = df06a7tab$week , y1= df06a7tab$poundsGT7,
             x2 = df06a7tab$week, y2 = df06b7tab$poundsGT7,
             ztitle = "PlotFour : Baby weight >= 7lbs versus Baby weight < 7lbs",
             zlegendText = c("Baby weight >= 7lbs","Baby weight < 7lbs")
)

####PlotFive 
#head(df02,20)
df70s <-df02[df02$motherbirthyear > 1970 & df02$motherbirthyear <=1979,c("week","motherbirthyear")]
df80s <-df02[df02$motherbirthyear > 1980 & df02$motherbirthyear < 2019,c("week","motherbirthyear")]

df70s <-df70s[df70s$week >= 35.00 & df70s$week <= 43.00,]
df80s <-df80s[df80s$week >= 35.00 & df80s$week <= 43.00,]

#aggregate tables
df70stab <- aggregate(motherbirthyear ~ week,FUN = length,df70s)
df80stab <- aggregate(motherbirthyear ~ week,FUN = length,df80s)

#normalization
counter <- sum(df70stab$motherbirthyear)+ 10
df70stab$motherbirthyear <- df70stab$motherbirthyear/counter
counter <- sum(df80stab$motherbirthyear)+ 10
df80stab$motherbirthyear <- df80stab$motherbirthyear/counter

#PlotFive: Mothers whose birth year is in the 1970s, versus mothers whose birthyear is 1980s or later.
ztitle <- "PlotFive: Mothers whose birth year is in the 1970s, versus mothers whose birthyear is 1980s or later."
plotFunction(x1 = df80stab$week , y1= df80stab$motherbirthyear,
             x2 = df70stab$week, y2 = df70stab$motherbirthyear,
             ztitle= ztitle,
             zlegendText = c("birth year is in the 1980s","birth year is in the 1970s")
)

####Que 3
#Calculate the sample mean and standard deviation of the born-on date, and use the dnorm()
#command to overlay a normal distribution plot on a plot like you generate above,
#excluding observations excluded from the charts. Does the normal distribution 
#provide a useful description of the likelihood a baby is born before the due date?
#Does the normal distribution provide a useful description of the likelihood a baby
#is born after the due date?

#mean & Sd
mean1 <- mean(df02[df02$week >= 35.00 & df02$week < 43.00,"week"])   #39.77773
sd1 <- sd(df02[df02$week >= 35.00 & df02$week < 43.00,"week"])       #1.417654

#grid
x1 = 3500:43/7 #grid, increment in 7th  # from Website, group discussion
mean1 = mean(df05$week)
sd1 = 9.57/7
d <- dnorm(x1, mean = mean1, sd = sd1)
d <- d/sum(d)
#plotSix
plotFunction(x1 = df05Lmp$week, y1 = df05Lmp$LMP,
             x2 = df05ovulation$week , y2= df05ovulation$ovulation,
             x3 = df05ultrasound$week, y3= df05ultrasound$ultrasound,
             ztitle = "PlotSix : Born on date",
             zlegendText = c("LMP","Ovulation", "Ultrasound")
)
lines(x = x1, y = d
            ,type= "o"
            ,col = "black"  #black #color of the line chart
            ,lty = "dashed"                  #line thickness
           # ,pch = 0                  # add points, solid circle,
            ,cex = 0.3                 # size of the point on the chart
)

###global adjustments start 2
options(warn = oldwarnval) #reset the warning message
###global adjustments end 2